فئات: مقالات مميزة » كهربائيين المبتدئين
مرات المشاهدة: 92355
تعليقات على المقال: 1
الجبر المنطقي. الجزء 2. القوانين والوظائف الأساسية
 استمرار القصة حول الجبر المنطقي والاتفاقيات والقواعد والعمليات. الانتقال إلى أساسيات دوائر الاتصال.
استمرار القصة حول الجبر المنطقي والاتفاقيات والقواعد والعمليات. الانتقال إلى أساسيات دوائر الاتصال.
ال المادة الأولى تم وصف جورج بول بأنه خالق جبر المنطق. المقالة الثانية سوف تصف العمليات الأساسية للجبر المنطقي ، وأساليب تبسيط التعبيرات المنطقية. لذلك ، يستخدم الجبر المنطقي العبارات كحجج ، وليس معناها ، ولكن الحقيقة أو زيف البيان.
شكل لكتابة التعبيرات في الجبر المنطقي.
إذا كان البيان صحيحًا ، فسيتم كتابته على النحو التالي: A = 1 ، إذا كان خاطئًا ، ثم A = 0 (بعد كل شيء ، ليس صحيحًا أن البطاطا هي ثمرة). لأي عبارة ، A إما صحيحة (A = 1) أو خاطئة (A = 0). لا يمكن أن يكون هناك وسط هنا. لقد تحدثنا بالفعل عن هذا.
إذا قمت بتوصيل بيانين بسيطين بالاتحاد ، فستحصل على بيان معقد ، يُسمى المنتج المنطقي. دعنا نأخذ كلمتين بسيطتين: "ثلاثة أكثر من اثنين" ، سنقوم بتعيين بواسطة الحرف A ، "ثلاثة أقل من خمسة" - بالحرف B.
ومن هنا فإن العبارة المعقدة "ثلاثة أكثر من اثنين وأقل من خمسة" هي عبارة منطقية (في هذه الحالة ، الحرف الكبير و ، تقول أن هذه عملية منطقية "AND" ، وكذلك لاحقًا في النص "OR" و "NOT".) و B. تم تعيينه على النحو التالي: A ^ B أو A * B.
الضرب المنطقي (العملية "AND").
في الجبر الابتدائية A * A = A2. ولكن في جبر Buhl ، A * A = A2 = A ، A * A = A ، لأن علامة الضرب (*) تعني الآن ... و ... بمعنى And ... و. جميع تجربتنا تؤكد أن A&A هو نفسه A. وحده لا يمكن للمرء أن يختلف مع هذا. حقيقة البيان لا تتغير إذا تكررت بالعامل عدة مرات.
يُعتبر ناتج بيانين صحيحًا (يساوي 1) ، وفقط إذا كان كلا العاملين صحيحين ، وخطأ (يساوي 0) إذا كان أحد العوامل على الأقل خطأ. توافق على أن هذه القواعد لا تتعارض مع المنطق السليم ، وبالإضافة إلى ذلك ، تمتثل امتثالًا تامًا لقواعد الجبر الأولية:
1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.
تقرأ المساواة الأولى كما يلي: إذا كان كل من A و B صحيحًا ، فسيكون المنتج A * B صحيحًا. في Buhl الجبر ، علامة الضرب (*) تحل محل الاتحاد الأول
قد لا تشمل المنتجات المنطقية اثنين ، ولكن عدد أكبر من العبارات - العوامل. وفي هذه الحالة ، يكون المنتج صحيحًا فقط عندما تكون جميع عوامل العبارات صحيحة في نفس الوقت.
الجمع المنطقي (أو العملية)
إذا كان هناك بيانان متصلان بنقابة أو. تلك الجملة المركبة المركبة تسمى المجموع المنطقي.
النظر في مثال على مجموع منطقي. قول A: "اليوم سأذهب إلى السينما."
البيان ب: "اليوم سأذهب إلى الديسكو". نضيف كلا البيانين ونحصل على: "اليوم سأذهب إلى السينما أو إلى الديسكو".
يُشار إلى هذا البيان المعقد على النحو التالي: A + B = C أو (A V B) = C.
بواسطة C أشرنا إلى بيان معقد للمبلغ المنطقي.
في المثال قيد النظر ، لا يمكن استخدام الاتحاد OR بالمعنى الحصري. في الواقع ، في نفس اليوم يمكنك الوصول إلى السينما وإلى الديسكو. وهنا يقول المثل:
"سيكون رئيس شراكة البستنة هو بتروف أو إيفانوف" ، ليس مبلغًا منطقيًا ، لأن شخصًا واحدًا فقط سيكون الرئيس ، والآخر سيكون بستاني هواة عاديًا.
يتم اختيار علامة V للمجموع المنطقي لأنه الحرف الأولي للكلمة اللاتينية "vel" ، ومعنى "أو" ، على عكس الكلمة اللاتينية "aut> ، والتي تعني" و ". الآن يجب أن يكون واضحًا للجميع لماذا يتم الإشارة إلى المنتج المنطقي بواسطة العلامة ^.
في الجبر الابتدائية هناك قاعدة A + A = 2A. هذه القاعدة صحيحة ، بغض النظر عن الرقم الذي يمثله الحرف A. في الجبر المنطقي ، تتطابق مع القاعدة A + A = A ، وتجربتنا في الحياة كلها تقول أن قول A أو A أو كلاهما A هو مجرد طريقة أخرى وأطول لنقول فقط A.
مثل أي بيان مركب ، يمكن أن يكون مجموع البيانين A و B صحيحًا أو خطأ. يُعتبر المجموع صحيحًا ، أي مساوًا للوحدة ، إذا كان واحدًا على الأقل من المصطلحات صحيحًا:
A + B = 1 إذا أو A = 1 أو B = 1 ، والذي يتسق مع الحساب التقليدي:
1+0 = 0+1 = 1.
إذا كانت كلتا الجملتين المجموعتين صحيحتين ، فسيتم اعتبار المجموع صحيحًا أيضًا ، لذلك ، في الجبر المنطقي لدينا: (1) + (1) = 1.
يتم تعيين الأقواس هنا من أجل التأكيد على الشرطية ، معنى هذه الإضافة ، وليس الحساب.
يعتبر مجموع البيانين خاطئًا ويساوي الصفر إذا ، لكن فقط إذا كان كلا المصطلحين خاطئين. من هنا:
0 + 0=0.
لذلك ، يعتبر مجموع البيانين A + B صحيحًا إذا كان true ، أو A A ، أو B ، أو كلا المصطلحين معًا. وبالتالي ، يتم الإشارة إلى الكلمة OR بواسطة +.
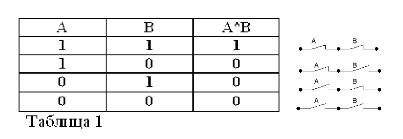
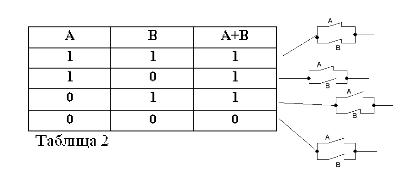
تذكر أن العبارات A و B يمكن أن تكون صحيحة أو خاطئة فقط ، وبالتالي ، لها مقياس للحقيقة 1 أو 0 ، يمكن تلخيص نتائج العمليات AND و OR المدروسة في الجدولين 1 و 2.
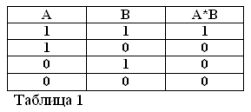
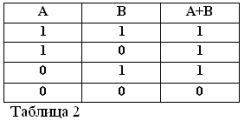
العملية الثالثة ، المستخدمة على نطاق واسع من قبل الجبر Buhl ، هي عملية النفي - لا. نذكرك أن الجبر الأولي يستخدم العمليات ADD و D الطرح والضرب والقسمة والبعض الآخر.
لكل عبارة A ، يوجد نفي لها NOT A ، والذي سنشير إليه بالرمز / A. هذا لا ينبغي أن يكون موضع شك.
نعطي أمثلة: "سوف نذهب إلى الغابة" أ ، "لن نذهب إلى الغابة" / أ.
إذا كانت العبارة A صحيحة ، أي ، A = 1 ، فعندئذ يجب أن تكون نفيها / A خاطئة / A = 0. والعكس صحيح ، إذا كان أي بيان خاطئًا ، فإن نفيه يكون صحيحًا. على سبيل المثال: "الحصان لا يأكل القش" / A = 0 ، "الحصان لا يأكل القش" (A = 1). ويمكن التعبير عن ذلك في الجدول 3.
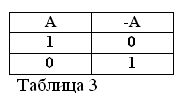
تحديد معنى فعل النفي ، وافتراض أن البيانين A و / A هو دائمًا صيغة واحدة حقيقية ، صيغتان جديدتان لجبر Boolean:
A + (/ A) = 1 و A * (/ A) = 0.
هناك أيضًا صيغ أخرى تبسط المعالجة المنطقية للبيانات. على سبيل المثال ، 1 + A = 1 ، لأنه ، وفقًا لتعريف الجمع ، في الحالة التي يكون فيها مصطلح واحد مساوياً للوحدة ، يكون المجموع مساويًا دائمًا للوحدة. النتيجة التي تم الحصول عليها لا تعتمد على ما إذا كانت A = 0 أو A = 1.
كل من العمليات المنطقية الثلاث التي درسناها (AND ، OR ، NOT) لها خصائص معينة قريبة من قواعد الجبر الأولي. إذا تمت صياغة جميعها ، فسنحصل على 25 قاعدة من الجبر المنطقي. فهي كافية لحل أي مشكلة منطقية تقريبًا. بدون هذه القواعد ، يصبح حل المشكلات المنطقية أمرًا صعبًا للغاية بسبب تعقيدها الظاهر. محاولة العثور على الإجابة الصحيحة دون استخدام القواعد يعني استبدالها بالإبداع والتفكير العام. قواعد تسهل كثيرا هذا العمل وتوفير الوقت.
في إطار المقال ، من المستحيل النظر في جميع هذه القواعد الـ 25 ، لكن أولئك الذين يرغبون في العثور عليها دائمًا في الأدبيات ذات الصلة.
كما ذُكر سابقًا في المقالة الأولى في عام 1938 ، استخدم العالم الأمريكي الشاب كلود شانون في مقالته "التحليل الرمزي لدارات الترحيل والتبديل" لأول مرة الجبر البوليني لمشاكل تقنية الترحيل. كان اكتشاف شانون هو أنه أدرك أن طريقة تصميم أجهزة الترحيل وأجهزة الكمبيوتر الإلكترونية هي في الواقع فرع من المنطق الرياضي.
غالبا ما يحدث. لسنوات عديدة ، كان العالم يعمل على مشكلة تبدو غير ضرورية على الإطلاق لمواطنيه - إنها مجرد متعة. ولكن بعد مرور عقود وأحيانًا على قرون ، ونظرية لا يحتاج إليها أحد لا تكتسب حق الوجود فقط ، ولكن بدونه يصبح التقدم الإضافي غير وارد.
ما الذي ساعد شانون للمرة الثانية على "اكتشاف" الجبر المنطقي؟ هذه القضية؟ لا شيء من هذا القبيل.
ساعد حب آلات الترحيل ، المبنية على مفاتيح التبديل والتتابع التقليدية ، العالم الشاب على توصيل النظرية المنسية بمهام التبادلات الهاتفية التلقائية ، والتي عمل عليها في ذلك الوقت. بعد ذلك ، قدم شانون نفس فكرة "نعم أو لا" في رسائل منفصلة ووضع الأساس لقسم كامل من علم التحكم الآلي - نظرية المعلومات.
كانت جبر Buhl مناسبة للغاية لتحليل وتوليف دوائر الترحيل. كان يكفي أن نقبل كبيان حقيقي: "هناك إشارة في الدائرة" ، وكإشارة خاطئة - "لا توجد إشارة في الدائرة" ، كما ظهر جبر جديد - جبر الإشارة ، جبر دائرة الترحيل.
الجبر الجديد صالح فقط للنظر في دوائر التتابع والتبديل. بعد كل شيء ، فقط في مثل هذه المخططات هو الشرط "هناك إشارة" و "لا توجد إشارة" بالارتياح. عندما تتغير الإشارة باستمرار ، والحصول على عدد كبير بشكل تعسفي من الحالات الوسيطة (مثل هذه الإشارة تسمى التناظرية) ، لا تنطبق جبر الترحيل. يجب دائما أن نتذكر هذا. لكن غالبية أجهزة الكمبيوتر الإلكترونية والأجهزة السيبرانية تستخدم المبدأ المنفصل لمعالجة الإشارات ، والذي يعتمد على عناصر "نعم - لا".
تم قبول تعبير "Contact Closed" من قبل Shannon على أنه صحيح (1) ، و "Contact open" على أنه false (0). ما تبقى من "الجبر" ، بما في ذلك العمليات و ، OR و NOT و 25 قواعد ، شانون مقترضة من بول.
تحولت جبر دائرة الترحيل إلى أنها أبسط من جبر Boolean ، حيث إنها تتعامل فقط مع عناصر من النوع "yes - no". بالإضافة إلى ذلك ، فإن الجبر الجديد هو أكثر البصرية.
العناصر الموجودة في هذه الجبر هي جهات الاتصال ، والتي سنشير إليها بالحروف A ، B ، C ... جهة الاتصال مغلقة - A ، جهة الاتصال مفتوحة - / A (رسالة مع شرطة).
التدوين ، كما ترى ، مأخوذ تمامًا من الجبر المنطقي. جهة اتصال مفتوحة هي نفي لجهة اتصال مغلقة. لا يمكن أن تكون جهة الاتصال نفسها مغلقة ومفتوحة.
دعنا نتفق على أنه في أي دائرة يتم الإشارة إلى جهات اتصال بحرف واحد ، فإن هذا يعني أنهم يأخذون دائمًا نفس القيم.
في أي لحظة ، يكون كلاهما مفتوحًا في نفس الوقت ، أو كلاهما مغلق. أسهل طريقة لتخيلهم مرتبطة ميكانيكيا معًا بحيث يكون كلاهما مفتوحًا أو قريبًا.
إذا كانت جهة الاتصال في بعض السلسلة هي نفي لجهة اتصال أخرى ، فإن معانيها تكون معاكسة دائمًا. على سبيل المثال ، لا يمكن مطلقًا فتح جهات الاتصال C و / C في وقت واحد أو إغلاقها في وقت واحد. وفي المخطط ، يمكن تمثيلهم بشكل ميكانيكي: إذا فتح أحدهم ، فسيتم إغلاق الآخر.
نبدأ في التعرف على جبر الترحيل من خلال تحليل أبسط الدوائر المقابلة لعمليات AND و OR و NOT.
منتج جهة اتصال اثنين (العملية AND) هو الدائرة التي يتم الحصول عليها نتيجة لاتصال السلسلة: يتم إغلاقه (يساوي 1) فقط عندما تكون كلتا جهات الاتصال مغلقة (تساوي 1).
سيكون مجموع جهات الاتصال (OR العملية) هو الدائرة التي يتم تشكيلها عند توصيلها بالتوازي: تكون مغلقة (تساوي 1) عندما يكون واحد على الأقل من جهات الاتصال التي تشكل الدائرة مغلقًا (يساوي 1).
الجهة المقابلة لجهة الاتصال هذه (العملية NOT) هي جهة اتصال تساوي 0 (مفتوحة) إذا كانت جهة الاتصال هذه (مغلقة) ، والعكس صحيح.
كما هو الحال في الجبر المنطقي ، إذا تمت الإشارة إلى جهات الاتصال بالحرفين A و B ، فسنشير إلى المنتج الخاص بجهات اتصال بواسطة A * B ، والمجموع A + B ، والجهة المقابلة A ، by / A. ما ورد أعلاه موضح في الأشكال 1 و 2 و 3.
صلاحية الجداول المقابلة لعمليات AND و OR و NOT. الآن لا ينبغي لأحد أن يكون في شك.
دعونا نتناول مثالين: 1 * 0 = 0 و 1 + 0 = 1.
يمكن ملاحظة من الشكل أن جهة اتصال مغلقة نهائيًا متصلة في سلسلة مع جهة اتصال مفتوحة بشكل دائم تعادل جهة اتصال مفتوحة نهائيًا (1 * 0 = 0) جهة اتصال مغلقة نهائيًا متصلة بالتوازي مع جهة اتصال مفتوحة بشكل دائم تعادل جهة اتصال مغلقة دائمًا.
بعد التعرف على حساب دوائر الاتصال ، يمكنك وصف أي دائرة ترحيل مع صيغة باستخدام الاتفاقيات المقبولة. في علم التحكم الآلي ، تسمى هذه الصيغ هيكلية.
إذا كانت الصيغة الهيكلية لأي دائرة ترحيل هي 1 ، فيمكن أن تمر الإشارة عبرها - تكون الدائرة مغلقة. على العكس ، إذا كانت الصيغة الهيكلية للدائرة تساوي 0 ، فلن تمر الإشارة عبرها - فالدائرة مكسورة.الخلاصة: دائرتا مرحلتان تعادلان بعضهما البعض عندما تكون الصيغ الهيكلية متساوية.
في متابعة المقال ، سننظر في أمثلة على دوائر الاتصال ودارات الاتصال النموذجية وما يعادلها ، وكذلك رسم المخططات وفقًا للصيغ الهيكلية. نعتبر أيضًا الدوائر المنطقية الرئيسية التي تؤدي وظائف الجبر المنطقي.
استمرار المقال: الجبر المنطقي. الجزء 3. مخططات الاتصال
بوريس الأديشين
انظر أيضا في electro-ar.tomathouse.com
: