الجبر المنطقي. الجزء 1. قليلا من التاريخ

في المدرسة ، درسنا جميعًا الجبر ، لكنهم لم يتحدثوا عن الجبر المنطقي هناك. ما هو الفرق بين الجبر المنطقي والجبر المدرسي ، تاريخ ظهوره والمشاكل والتطبيقات الموضحة في هذه المقالة.

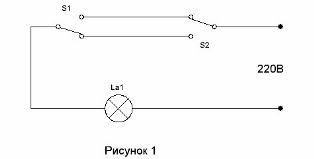
الدائرة التي تسمح لمفتاحين بتشغيل الضوء في الممر عند مدخل الممر وإيقاف تشغيله عند دخول الغرفة كانت معروفة لفترة طويلة جدًا (انظر. دائرة التحكم في الإضاءة الممر). يظهر في الشكل 1.

المهمة رقم 1. أكثر تعقيدا. قم بإنشاء رسم بياني يسمح لك بتشغيل وإطفاء الضوء في غرفتك باستخدام أي من مفاتيح التبديل الثلاثة المختلفة. توجد المفاتيح عند مدخل الغرفة وفوق السرير وفي المكتب.

المهمة رقم 2.

في لجنة رياضية ، مثل لجنة المصانع ، تجمع 5 قضاة.

يجب على كل منهم التصويت لصالح قرارات مختلفة. يتم اتخاذ القرار بأغلبية الأصوات ، ولكن بشرط إضافي أن يصوت رئيس اللجنة لصالحه.

يصوت الحكام بالضغط على الزر الذي يغلق المفتاح الموجود أسفل الطاولة التي يجلسون عليها. إغلاق التبديل ، يصوتون لصالح ، فصل سلبيات. ارسم مخططًا بسيطًا يسمح لك بمشاهدة نتائج التصويت تلقائيًا. في أبسط الحالات ، وببساطة بمساعدة مصباح كهربائي - مضاءة - تم اتخاذ القرار ، ولم يضيء - لا.

المهمة رقم 3. في الممارسة العملية ، هذا غير مرجح ، ولكن كمهمة تعليمية معقدة مناسبة تمامًا.

في غرفة سداسية كبيرة ، يتم تثبيت مفتاح واحد على كل جدار. قم ببناء دائرة بحيث يمكنك في أي وقت تشغيل أو إيقاف تشغيل الضوء في الغرفة عن طريق تشغيل مفتاح واحد (أي).

بعد الجلوس دون جدوى في المهام لمدة ثلاثة إلى أربعة أيام ، ضعها جانباً مؤقتًا. وانشغل الجبر المنطقي. إنه الجبر المنطقي ، أو ، كما يطلق عليه أيضًا ، الجبر المنطقي ، جبر دائرة التتابع، سوف تساعدك على حل مشاكلك.

ما هو الجبر المنطقي؟

ومن الغريب أنه على الرغم من حقيقة أنهم يدرسون الجبر لمدة خمس سنوات في المدرسة ، فإن العديد من الطلاب ، والكبار في وقت لاحق ، لن يكونوا قادرين على الإجابة على السؤال ، ما هي الجبر؟ الجبر هو العلم الذي يدرس مجموعات من بعض العناصر والإجراءات المتعلقة بها.

في دورة مدرسية في الجبر ، هذه العناصر عبارة عن أرقام. يمكن الإشارة إلى الأرقام ليس بالأرقام ، ولكن بالأحرف ، يكون الجميع على دراية بذلك. في الدروس الأولى للجبر ، يجعل هذا الأمر دائمًا من الصعب على العديد من الطلاب. تذكر كم كان من الصعب في البداية التعود على طي الحروف بدلاً من الأرقام ، وحل المعادلات التي لم تقل شيئًا.

من المحتمل أن كل واحد منا سأل أنفسنا السؤال التالي: "لماذا نحتاج إلى إدخال أحرف بدلاً من الأرقام وهل هذا ضروري على الإطلاق؟" وفي وقت لاحق فقط ، هل رأيت المزايا التي يوفرها الجبر عند حل المشكلات مقارنةً بالحساب.

يستخدم الجبر في العديد من العلوم الدقيقة. هذه هي الفيزياء ، الميكانيكا ، سوبرومات ، الكهرباء. قانون أوم لا يوجد أكثر من معادلة جبرية: يكفي استبدال قيمها العددية بدلاً من الحروف لمعرفة ما الذي سوف يتدفق التيار في الحمل ، أو ما هي المقاومة التي يملكها قسم من الدائرة.

لذلك تعرفت على جبر الأرقام ، أو الجبر الأولي. تتمثل المهمة الرئيسية والفريدة تقريبًا في الحصول على إجابة على السؤال: "ما هي علامة X؟ كم؟

في المدرسة الثانوية ، يدرسون بدايات الجبر المتجه. هذه الجبر تختلف اختلافًا جذريًا عن الجبر الأولي. له طبيعة مختلفة للمجموعة المدروسة وقواعد العمل الأخرى. حل معادلة المتجه ، نحصل في الإجابة على متجه ليس رقماً عادياً يجيب على السؤال "كم؟"

تختلف صيغ الجبر المتجه في كثير من النواحي عن صيغ الجبر الأولي. على سبيل المثال ، في الجبر الأولي وفي الجبر المتجه ، هناك عملية إضافة. ولكن يتم تنفيذها بطرق مختلفة تماما.إضافة الأرقام ليست على الإطلاق إضافة ناقلات.

هناك جبر أخرى: الجبر الخطي ، جبر الهياكل ، جبر الخواتم ، جبر المنطق ، أو ، ما هو نفسه ، الجبر المنطقي. ربما لم تسمع الاسم في دروس المدرسة. جورج بول - لكن الجميع يعرف اسم إحدى بناته الموهوبين إثيل فوينيتش (1864 - 1960). كتبت رواية "Gadfly" ، التي تتحدث عن الكفاح من أجل حقوق الكربانيين الإيطاليين.

ولد جورج بول في إنجلترا في الثاني من نوفمبر عام 1815. طوال حياته ، عمل مدرسًا للرياضيات والفيزياء في المدرسة. من مذكرات طلابه ، من المعروف الأهمية الكبرى التي يوليها بول لتطوير قدرات الطلاب الإبداعية. في تقديمه مواد جديدة ، سعى إلى التأكد من أن طلابه أنفسهم "اكتشفوا" بعض الصيغ والقوانين.

لإخبار الطلاب عن الصعوبات التي واجهها العلماء حتما في البحث عن الحقيقة ، أحب المعلم أن يكرر حكمة شرقية واحدة: حتى العرش الفارسي لا يمكن أن يجلب الكثير من المتعة لشخص مثل أصغر اكتشاف علمي. لم يفقد بوهل الأمل في يوم من الأيام أن يقوم طلابه باكتشاف حقيقي.

كان نطاق الاهتمامات العلمية لبول واسعًا جدًا: كان مهتمًا على قدم المساواة بالرياضيات والمنطق - علم القوانين وأشكال التفكير. في تلك الأيام ، كان المنطق يُعتبر علمًا للإنسانيات ، وكان الكثيرون ممن يعرفون جورج بول مندهشين من الطريقة التي يمكن أن تتعايش بها طرق الإدراك الدقيقة المتأصلة في الرياضيات والطرق الوصفية البحتة للمنطق في شخص واحد.

لكن العالم أراد أن يجعل علم القوانين وأشكال التفكير صارمة مثل أي من العلوم الطبيعية ، كما يقول الرياضيات والفيزياء. لهذا ، بدأ بول يفيد ليس بالأرقام كحرف ، كما هو الحال في الجبر العادي ، ولكن البيانات ، وأظهر أن مثل هذه المعادلات ، التي تشبه إلى حد كبير المعادلات الجبرية ، يمكن أن تحل أسئلة حول حقيقة وزيف التصريحات التي أدلى بها الإنسان. لذلك نشأت الجبر المنطقي.

ولكن قبل فترة طويلة من طرح جورج بوهول ، عالم الرياضيات والفيلسوف الألماني غوتفريد لايبنيز (1646-1716) فكرة إنشاء علم من شأنه أن يحدد جميع مفاهيم الخطاب العامي العادي مع الرموز ويؤسس بعض الجبر الجديد لدمج هذه الرموز.

بعد ابتكار مثل هذا العلم ، وفقًا لما قاله ليبنيز ، سيتوقف العلماء والفلاسفة عن المجادلة والصراخ لبعضهم البعض ، ويكتشفون الحقيقة ، لكنهم سوف يلتقطون قلمًا ويقولون بهدوء: "دعنا نحسب!"

اليوم ، أصبحت جبر المنطق جزءًا مهمًا من الرياضيات. تتمثل إحدى مهامها في حل جميع أنواع المعادلات ، حيث يتم استبدال النسب العددية بحرف واحد. ربما تذكر كل واحد منكم طوال حياتك كيفية حل معادلات الدرجة الثانية والثالثة بمعاملات الحروف. لذلك ، استخدم بول في جبره الجديد كل هذه الصيغ والقواعد.

ما الجديد في الجبر المنطقي هو أن عناصر المجموعة التي تمت دراستها فيه ليست أرقامًا ، بل بيانات. إذا ، عند حل المعادلات الجبرية العادية ، يتم تحديد العدد الذي يساوي المجهول X ، فإن جبر المدرسة يبحث عن إجابة للسؤال: "كم؟"

تبحث جبر المنطق عن إجابة السؤال: "هل هذا أو ذاك يدل على أن الحرف X صحيح؟"

لا يلعب معنى ومحتوى البيان أي دور هنا. كل عبارة يمكن أن تكون صحيحة أو خاطئة. لا يمكن أن يكون نصف صحيح ونصف كاذبة. على سبيل المثال ، يمكننا أن نتذكر القذف بالعملة المعدنية.

ولا يوجد سوى دولتين يعملان بالعملة المعدنية - هناك رؤوس أو ذيول. باتفاق الطرفين ، النسر هو نعم ، وذيول لا. لا تؤخذ أي نقاط وسيطة أخرى في الاعتبار في نظرية الاحتمالات ، على الرغم من أنها ممكنة. يمكن أن تسقط العملة المعدنية المقلوبة على الحافة ، وتدحرج الأرضية إلى أرجل الكرسي أو الطاولة وتبقى في وضع مستقيم ، أو قد تقع في فجوة واسعة في الأرضية. (عن طريق القياس مع الدوائر الكهربائية ، يمكن اعتبار الحالتين الأخيرتين بمثابة عطل في شكل اتصال محترق).ولكن في تلك الأيام ، لم تستخدم الجبر البوليني ، للأسف ، على نطاق واسع.

كلود شانون "اكتشف" جبر Buhl مرة أخرى. في عام 1938 ، بينما كان لا يزال طالبًا في معهد ماساتشوستس للتكنولوجيا وأمريكا ، أثبت كلود الشاب أن جبر بوليان مناسب تمامًا لتحليل وتوليف دوائر الترحيل والتبديل.

بمساعدة الجبر Boolean ، من السهل جدًا عمل دائرة كهربائية لأوتوماتون تعمل على مرحل.فيما يتعلق بهذا ، اتضح أنك تحتاج فقط إلى معرفة بالضبط ما يجب أن يفعله الجهاز ، أي أنك بحاجة إلى خوارزمية لتشغيلها. لذلك تم وضع الأساس لنظرية الأجهزة الرقمية التي تعمل على مبدأ نعم أو لا.

هذا ، باختصار ، هو تاريخ الجبر المنطقي. في المقالات التالية ، سننظر في قوانينها الأساسية ، أمثلة على دوائر الاتصال التي تنفذ هذه القوانين. النظر في حل تلك المهام التي تم إعطاءها في بداية المقال.

استمرار المقال: الجبر المنطقي. الجزء 2. القوانين والوظائف الأساسية

بوريس الأديشين