ما هي العلاقة بين أقسام الأسلاك والسكان الأرانب؟

في عام 1202 ، نشر عالم الرياضيات الإيطالي ليوناردو فيبوناتشي عمله تحت عنوان "كتاب العداد" ("كتاب الحسابات") ، والذي وصف فيه أيضًا سلسلة الأرقام التي خُلدت باسمه. في أحد الفصول ، يحاول فيبوناتشي إظهار كيفية زيادة عدد الأرانب حسابيًا. واعتبر الفرضيات التالية كشروط:

1) في الشهرين الأولين ، زوج من الأرانب لا يعطي ذرية ؛

2) ابتداء من الشهر الثالث ، زوج من الأرانب يعطي زوج آخر من الأرانب.

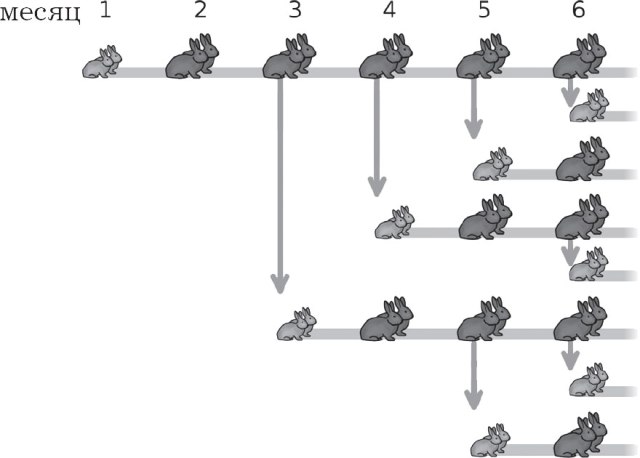
نتيجة لبناء نمط نمو عدد الأرانب ، نحصل على سلسلة الأرقام التالية ، مع ملاحظة الزيادة في عدد الأرانب كل شهر:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

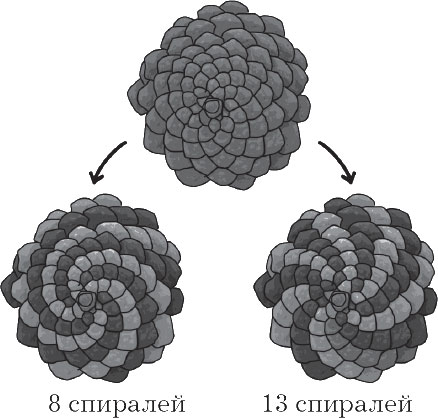
إذا نظرت بعناية إلى النتوء ، فسترى أن سطحه يتكون من موازين ملتوية في دوامة وفقًا لتسلسل فيبوناتشي. أثناء وجودها في الأناناس أو في زهرة عباد الشمس ، تكون مرئية للعين المجردة.

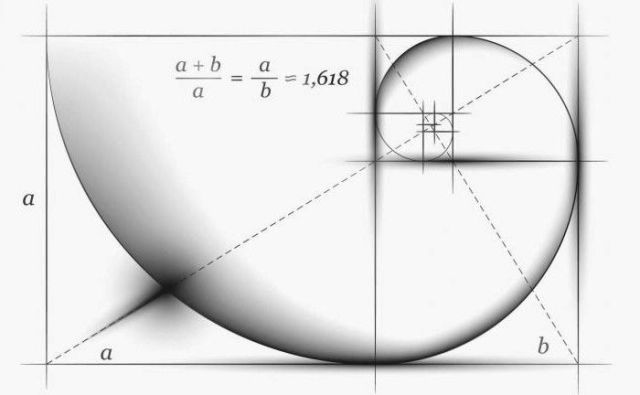
منذ زمن العصور القديمة للنسبة الذهبية - العدد = 1،618. نظر الإغريق القدماء في قيمة النسبة المثالية. النسبة الذهبية هي نسبة كل رقم لاحق في سلسلة فيبوناتشي إلى الرقم السابق:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

استخدمه الإغريق القدماء في الهندسة المعمارية. لواجهة البارثينون في أثينا أبعاد متشابهة للغاية مع مستطيل مبني على مبدأ النسبة الذهبية.

فما هو جمال تسلسل المقاطع العرضية للاسلاك ، والتيارات المقدرة للتيارات الكهربائية وقطع التيار الكهربائي لقواطع الدائرة الكهربائية؟ بناء سلسلة من الأرقام مع القيم التالية: 1،5؛ 2.5. (4)؛ 6؛ 10؛ 16؛ 25; 40; 63...

التيارات المقدرة من البداية الكهرومغناطيسية:

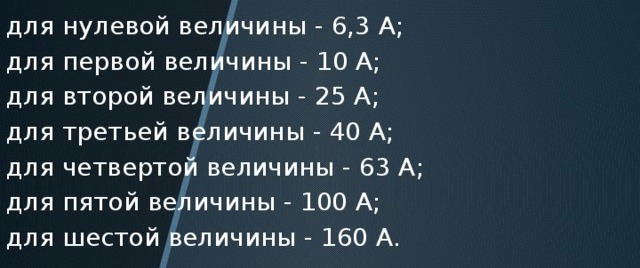
إذا قمت بتقسيم 2.5 / 1.5 ؛ 4 / 2.5 6.3 / 4 ؛ 10 / 6.3 ؛ 16/10. 25/16; 40/25; 63/40ثم نحصل على حوالي 1.6. وهو ما يتوافق مع قاعدة النسبة الذهبية. ويعكس جمال الطبيعة وعبقريتها حتى في النظم الهندسية المملة.

ما رايك هل هذا حادث؟

بناءً على كتاب "رواية عظيمة عن الرياضيات. تاريخ العالم من خلال منظور الرياضيات" بقلم مايكل لون. شكرا على توصية من فلاديمير كيسل.

أليكسي بوشنياجا